We can calculate the sum of N natural numbers using a loop or directly applying a formula. In this tutorial, we’ll explore both methods.
Approach 1: Using a Loop
Algorithm
- Start
- Assign sum=0 and i=0
- Read the number , n
- Repeat steps 5 to 6 until i=n reached
- Compute sum=sum+i
- Compute i=i+1
- Print sum
- Stop
Flowchart
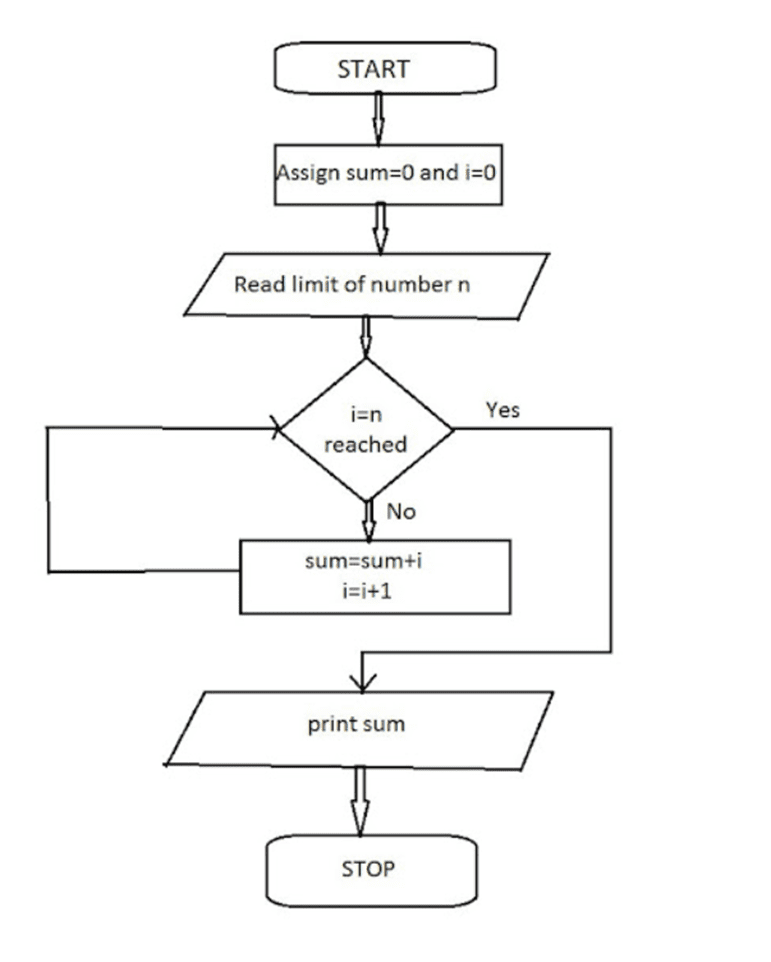
This approach involves initializing a sum variable to 0 and iterating through the numbers from 1 to n, accumulating the sum along the way.
Approach 2: Using a Formula
Algorithm
- Start
- Read the number n
- Calculate the sum of n natural number, sum = n * (n + 1) / 2
- Display sum
- End
Flowchart
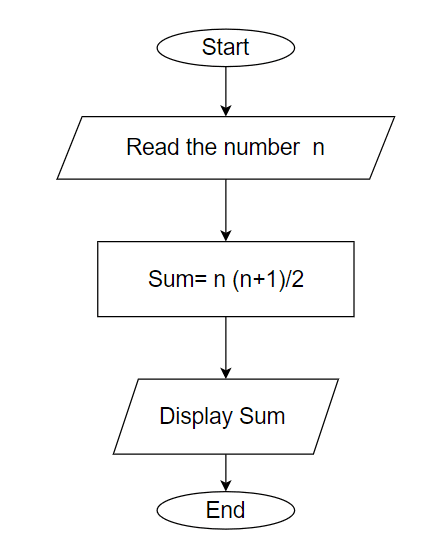
This approach directly applies the formula n (n+1)2 to calculate the sum of the first n natural numbers without the need for iteration. It’s a more efficient method since it avoids the overhead of a loop and an intermediate variable.
Conclusion
Both approaches provided the same result—the sum of the n natural numbers. However, the formula-based approach is more direct and efficient, making it preferable in many situations, especially when dealing with large values of n. However, understanding both methods is essential for a comprehensive understanding of programming logic and problem-solving techniques. Choose the approach that best suits your needs and the requirements of your specific problem.
Read also:
Algorithm And Flowchart To Find Whether A Number Is Prime Number Or Not
Algorithm And Flowchart To Find The Largest Number Among Three Numbers